[LBS位置服务学习2] RTree判断点在多边形内-Java版本


1.什么是RTree
待补充
2.RTree java依赖
rtree的java开源版本在GitHub上:R树-Java版本
上面有详细的使用说明
最新版本的maven依赖可在中央仓库查到:
maven仓库
这里我们使用0.8.7版本
<dependency>
<groupId>com.github.davidmoten</groupId>
<artifactId>rtree</artifactId>
<version>0.8.7</version>
</dependency>
3.使用
3.1创建R树
创建R树
RTree<String, Geometry> tree = RTree.minChildren(3).maxChildren(6).create();
创建R*树
R*树是R树的变种,是在节点分裂方法上做了改进的R树,这点后续再写篇博客详细介绍
这样,第一步创建R树操作就完成了,是不是很简单!!!
3.2 往R树插入数据
可插入4种空间数据:点、线、圆、矩形
Geometries.RectangleGeometries.circleGeometries.pointGeometries.line
为什么没有面数据呢?
面其实也是多个线的组合,只需要将多边形的边依次插入R树就行
tree = tree.add("testPoint", Geometries.point(116.0D, 32.0D));
3.3 删除R树里的数据
删除的时候需要匹配名称和地理信息
tree = tree.delete("testPoint", Geometries.point(116.0D,32.0D));
3.4 搜索
R树对空间信息的查找平均时间复杂度是O(logN),最坏情况下是O(N)
搜索方法返回的结果需要Observable泛型
或者返回Iterable类型
.toBlocking().toIterable();
4. 应用:判断点是否在多边形内
说明:R树是用外接矩形判断点是否在矩形框内,只能用作粗筛,因此粗筛了一遍后,还需要用射线法做精确判断。有关射线法判断点在多边形内的方法可自行搜索。
假设业务场景是:我有很多个多边形数据,如商场AOI数据。现在需要通过用户的经纬度坐标判断用户在哪个商场里,从而按地理位置精准给用户推荐周边店铺营销信息。
这里的输入就是用户经纬度,输出是用户所在的商场。
设计
上文说过,R树要存多边形只能存它的边数据。这样操作之后,一个多边形就是一棵R树了,但是搜索是在多个多边形里找到能命中的,因此还需要再加一层R树,即用每个多边形的外接矩形构建父R树。详细设计如下:
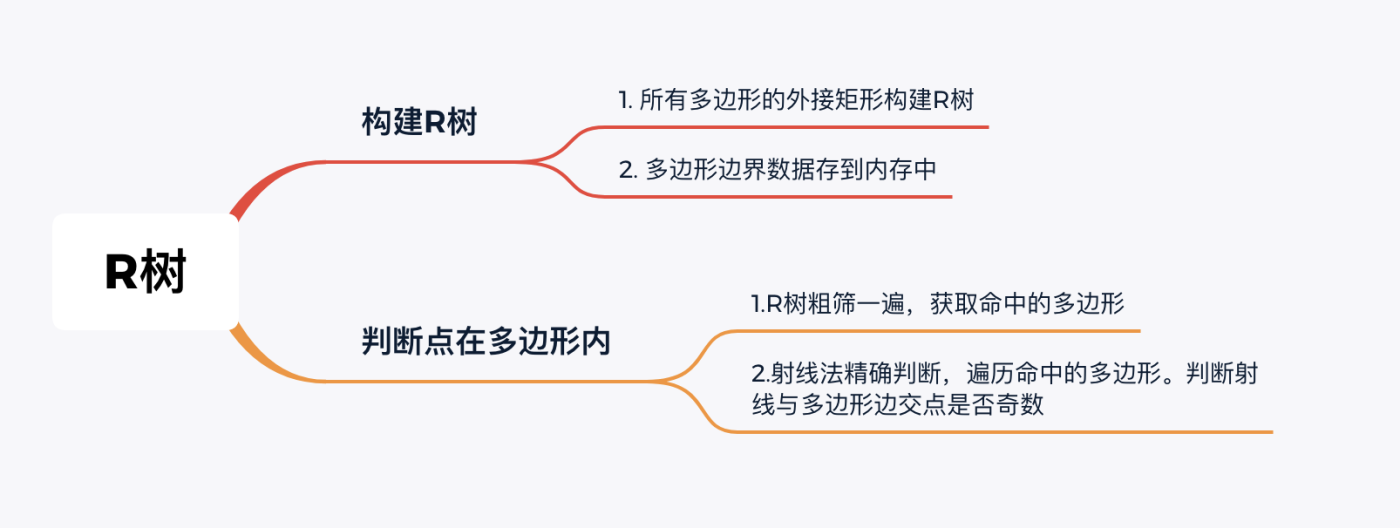
构建R树
具体逻辑如下:
private String dongcheng = "MULTIPOLYGON(((116.38059 39.871148,116.399097 39.872205,116.397612 39.898675,1116.38059 39.871148)))";
private String xicheng = "MULTIPOLYGON(((116.387658 39.96093,116.38678 39.957014,116.393346 39.957355,116.387658 39.96093)))";
private RTree<String, Rectangle> secondTree = RTree.minChildren(3).maxChildren(6).create();
public void build() {
List<CityDTO> sourceData = buildCityDTOs();
//1.对每个多边形,存入所有边构建一级R树
for (CityDTO sourceDatum : sourceData) {
RTree<String, Line> tree = RTree.minChildren(3).maxChildren(6).create();
List<List<Double>> polygon = GeoHelper.transfer2List(sourceDatum.getShape());
for (int i = 0; i < polygon.size(); i++) {
List<Double> nextPoints = polygon.get((i + 1) % polygon.size());
List<Double> points = polygon.get(i);
Double lng1 = points.get(0);
Double lat1 = points.get(1);
Double lng2 = nextPoints.get(0);
Double lat2 = nextPoints.get(1);
tree = tree.add(String.valueOf(i), Geometries.line(lng1, lat1, lng2, lat2));
}
//2. 将每个多边形的外接矩形构造为二级R树
secondTree = secondTree.add(sourceDatum.getName(), tree.mbr().get());
}
}
搜索
* 输入点坐标,查询命中的多边形name
* @param lng
* @param lat
* @return
*/
public String search(Double lng, Double lat) {
Point point = Geometries.point(lng, lat);
//r树粗筛一遍
Iterator<Entry<String, Rectangle>> iterator = tree.search(point).toBlocking().toIterable().iterator();
//射线法对粗筛的多边形精确计算
while (iterator.hasNext()) {
Entry<String, Rectangle> entry = iterator.next();
String name = entry.value();
//获取多边形wkt
String wkt = localShapeCache.get(name);
//射线法判断
PointDTO p = new PointDTO();
p.setLng(lng);
p.setLat(lat);
if (isInPolygon(p, GeoHelper.transfer2List(wkt))) {
return name;
}
}
return null;
}
射线法判断点在多边形内
* 射线法判断点是否在多边形内
* @param pointDTO
* @param polygon
* @return
*/
private boolean isInPolygon(PointDTO pointDTO, List<List<Double>> polygon) {
int nCross = 0;
for (int i = 0; i < polygon.size(); i++) {
List<Double> p1 = polygon.get(i);
List<Double> p2 = polygon.get((i + 1) % polygon.size());
Double lng1 = p1.get(0);
Double lat1 = p1.get(1);
Double lng2 = p2.get(0);
Double lat2 = p2.get(1);
//p1p2 与 y = p0.y平行
if (lng1.equals(lng2)) {
continue;
}
//交点在p1p2的延长线上
if (pointDTO.getLng() < Math.min(lng1, lng2)) {
continue;
}
//交点在p1p2的延长线上
if (pointDTO.getLng() >= Math.max(lng1, lng2)) {
continue;
}
// 求交点的X坐标
double x = (pointDTO.getLng() - lng1) * (lat2 - lat1) / (lng2 - lng1) + lat1;
if (x > pointDTO.getLat()) {
//只统计单边
nCross++;
}
}
//单边交点为奇数,点在多边形内
return (nCross % 2 == 1);
}
生成多边形的外接矩形
* 获取多边形的外接矩形
* @param wkt
* @return
*/
public Rectangle buildRectFromWkt(String wkt) {
double minLng = 180.00;
double minLat = 90;
double maxLng = -180.00;
double maxLat = -90.00;
//wkt格式数据转为点 list
List<List<Double>> polygon = GeoHelper.transfer2List(wkt);
for (List<Double> points : polygon) {
Double lng = points.get(0);
Double lat = points.get(1);
if (lng < minLng) {
minLng = lng;
}
if (lng > maxLng) {
maxLng = lng;
}
if (lat < minLat) {
minLat = lat;
}
if (lat > maxLat) {
maxLat = lat;
}
}
return Geometries.rectangle(minLng, minLat, maxLng, maxLat);
}
疑问没解决? 我们帮您!
如果您在本文中未能找到解决当前疑问的办法,不用担心――正睿专业技术支持团队随时待命

文章来源:阿里云开发者社区 作者:卷福同学